はじめに

検索チームの tumuzu です。画像生成などの技術的進歩は凄まじいですね。簡単なプロンプトから綺麗で多様なデータが生成されていて驚きっぱなしです。そこで拡散モデルの理論的なところが気になったので勉強して記事にしてみました。

この記事では拡散モデルから生成されたデータの質の高さの大きな要因であるサンプリング性能について見ていきます。拡散モデルのサンプリング性能の良さを体感するために、一般的なサンプリング法での問題点を確認しそれが拡散モデルと同等のモデルでは解決できていることを簡単な2次元データを使って見ていきます。

ちなみに『拡散モデルデータ生成技術の数理』という書籍を参考にしてます。わかりやすくてとてもいい本でした。日本語で書かれた詳しい説明が見たい方はおすすめです。

一部環境ではてなブログの数式が崩れて表示されるようです。数式を右クリックし、Common HTML を選択すると修正されます。参考 https://syleir.hatenablog.com/entry/2022/11/10/134211

サンプリング手法

真の分布からのサンプリング

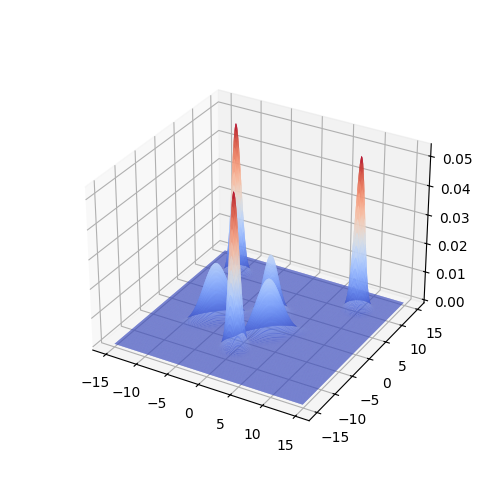
この記事では、6つの正規分布からなる以下の混合正規分布を真の分布 $p(x)$ とします。

$\displaystyle \frac{1}{6} \left[\mathcal{N} \left(\begin{bmatrix} -7.5 \\ 7.5 \end{bmatrix}, \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix} \right) + \mathcal{N} \left(\begin{bmatrix} 0 \\ -7.5 \end{bmatrix}, \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix} \right) + \mathcal{N} \left(\begin{bmatrix} 7.5 \\ 7.5 \end{bmatrix}, \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix} \right) + \mathcal{N} \left(\begin{bmatrix} 0 \\ 2.5 \end{bmatrix}, \begin{bmatrix} 1.25 & 0 \\ 0 & 1.25 \end{bmatrix} \right) + \mathcal{N} \left(\begin{bmatrix} -6 \\ -2.5 \end{bmatrix}, \begin{bmatrix} 2 & 1.5 \\ 1.5 & 2 \end{bmatrix} \right) + \mathcal{N} \left(\begin{bmatrix} 2.5 \\ -2.5 \end{bmatrix}, \begin{bmatrix} 2 & 1.5 \\ 1.5 & 2 \end{bmatrix} \right) \right] .$

コードではこのようになります。

class NormalDistribution:
    def __init__(self, mu, sigma):
        assert np.array_equal(sigma, sigma.T)
        self._mu = mu
        self._sigma = sigma

        self._inv_sigma = np.linalg.inv(sigma)
    
    def calc_prob(self, X):
        return multivariate_normal.pdf(X, mean=self._mu, cov=self._sigma)

class ContaminatedNormalDistribution:
    def __init__(self, dist_params_list):
        sum_ratio = sum([ratio for _, _, ratio in dist_params_list])
        epsilon = 0.0001
        assert 1.0 - epsilon < sum_ratio < 1.0 + epsilon
        mu0, sigma0, _ = dist_params_list[0]
        self._dist_list = []
        self._ratio_list = []
        for mu, sigma, ratio in dist_params_list:
            assert mu0.shape == mu.shape
            assert sigma0.shape == sigma.shape
            dist = NormalDistribution(mu, sigma)
            self._dist_list.append(dist)
            self._ratio_list.append(ratio)
    
    def calc_prob(self, X):
        prob = np.zeros(X.shape[0])
        prob_list = []
        for i, dist in enumerate(self._dist_list):
            ratio = self._ratio_list[i]
            tmp_prob = dist.calc_prob(X)
            prob += ratio * tmp_prob
            prob_list.append(tmp_prob)
        return prob, prob_list

dist_params_list = []

mu = np.array([-7.5, 7.5])
sigma = np.array([[0.5, 0],[0, 0.5]])
ratio = 1/6
dist_params_list.append((mu, sigma, ratio))

mu = np.array([0.0, -7.5])
sigma = np.array([[0.5, 0],[0, 0.5]])
ratio = 1/6
dist_params_list.append((mu, sigma, ratio))

mu = np.array([7.5, 7.5])
sigma = np.array([[0.5, 0],[0, 0.5]])
ratio = 1/6
dist_params_list.append((mu, sigma, ratio))

mu = np.array([0.0, 2.5])
sigma = np.array([[1.25, 0],[0, 1.25]])
ratio = 1/6
dist_params_list.append((mu, sigma, ratio))

mu = np.array([-6.0, -2.5])
sigma = np.array([[2, 1.5],[1.5, 2]])
ratio = 1/6
dist_params_list.append((mu, sigma, ratio))

mu = np.array([2.5, -2.5])
sigma = np.array([[2, 1.5],[1.5, 2]])
ratio = 1/6
dist_params_list.append((mu, sigma, ratio))

p = ContaminatedNormalDistribution(dist_params_list)

まずは、真の分布から直接サンプリングしてみます。

class NormalDistribution:
    ...
    def sample(self, N):
        return np.random.multivariate_normal(self._mu, self._sigma, N)

class ContaminatedNormalDistribution:
    ...
    def sample(self, N):
        dist_indexes = np.random.choice(len(self._ratio_list), N, p=[ratio for ratio in self._ratio_list])
        tmp_N_list = [np.count_nonzero(dist_indexes == i) for i in range(len(self._ratio_list))]
        samples = []
        for i, tmp_N in enumerate(tmp_N_list):
            samples.append(self._dist_list[i].sample(tmp_N))
        random.shuffle(samples)
        samples = np.concatenate(samples, axis=0)
        return samples

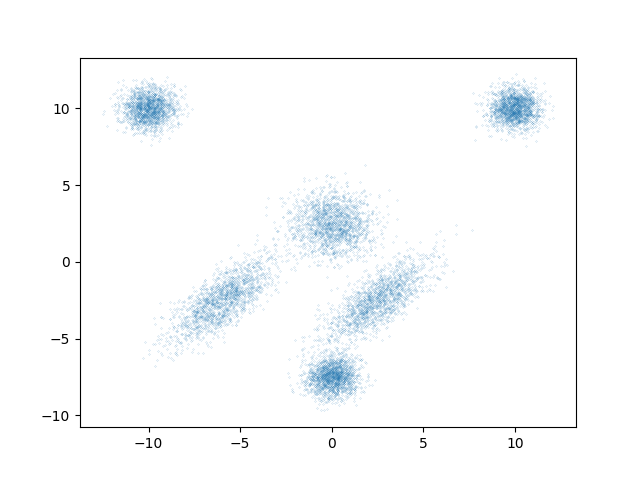
当たり前ですが、真の分布に従ったサンプリングができてます。

メトロポリス・ヘイスティングス法

実際にサンプリングする際には真の分布や確率はわからないが、尤度関数なら学習できることがあります。このようなときには代表的なMCMC法であるメトロポリス・ヘイスティングス法を使ってサンプリングできます。今回は尤度関数として真の確率密度関数をそのまま使ってサンプリングしてみます。

def metropolis_hastings(dist_params_list, X0, N, iter=1000):
    dim = 2
    p = ContaminatedNormalDistribution(dist_params_list)
    X = X0
    X_prob = p.calc_prob(X)
    epsilon = np.finfo(np.float32).tiny
    for j in range(iter):
        noise = np.random.normal(0, 1, (N, dim))
        X_candidate = X + noise
        X_prob = p.calc_prob(X)[0] + epsilon
        X_candidate_prob = p.calc_prob(X_candidate)[0] + epsilon
        acceptance_rate = np.minimum(1, X_candidate_prob * (1 / X_prob))
        rand = np.random.rand(N)
        X[rand < acceptance_rate] = X_candidate[rand < acceptance_rate]
    return X

X0 = np.random.normal(0, 1, (N, dim))
mh_sampled_X_snd_x0 = metropolis_hastings(dist_params_list, X0, 10000)

X0 = np.ones((N, dim))
X0[:, 0] = 100.0
X0[:, 1] = -100.0
mh_sampled_X_far_x0 = metropolis_hastings(dist_params_list, X0, 10000)

初期値 $x_0$ を $\mathcal{N}(\boldsymbol{0}, \mathrm{I})$ に従って生成した場合と、確率の低い領域からスタートするケースとして $[100, -100]^\top$ に固定した、両方のサンプリング結果を図に示します。

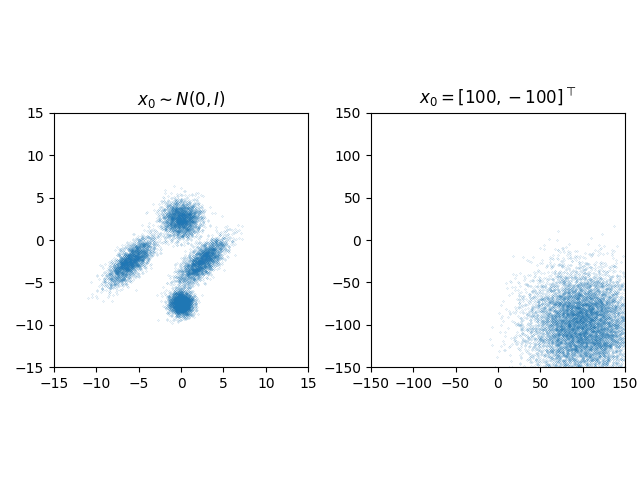
図から明らかなようにこのサンプリング方法には2つの問題点があります。１つは分布の山が複数あるような多峰性のデータ分布では、谷を乗り越えて他の山へ行くことが難しく、左側の図において右上と左上の山周辺のデータはほとんど生成されていません。2つ目はサンプリング性能が初期値に依存して効果的なサンプリングができない場合があることです。右側の図において尤度が低い領域に初期値を設定した場合に、尤度が高い領域へ移動できておらず意味のあるサンプリングになっていません。

スコアを用いたサンプリング

2つ目の問題点は、スコアと呼ばれる対数尤度 $\log p(x)$ の入力 $x$ についての勾配

$\displaystyle \nabla_{x} \log p(x) = \frac{\nabla_{x} p(x)}{p(x)} ,$

を用いたサンプリング方法で解決することができます。ある点のスコアはその位置から対数尤度が最も急激に大きくなる方向とその大きさを表しています。上の式を見ると分母に確率があり、確率が小さい領域で値が大きくなりやすいため、確率の小さい領域にあるデータからでも対数尤度が高い方向へ効率的に探索できます。このスコアを用いたランジュバン・モンテカルロ法と呼ばれるMCMC法を使ってサンプリングしてみます。

def langevin_monte_carlo(dist_params_list, X0, N, K=1000, alpha=0.1):
    dim = 2
    p = ContaminatedNormalDistribution(dist_params_list)
    noise_coeef = np.sqrt(2 * alpha)

    noise = np.random.normal(0, 1, (K, N, dim))
    for j in range(K):
        X = X + alpha * p.calc_score(X) + noise_coeef * noise[j]
    return X

X0 = np.random.normal(0, 1, (N, dim))
lm_sampled_X_snd_x0 = langevin_monte_carlo(dist_params_list, X0, 10000)

X0 = np.ones((N, dim))
X0[:, 0] = 100.0
X0[:, 1] = -100.0
lm_sampled_X_far_x0 = langevin_monte_carlo(dist_params_list, X0, 10000)

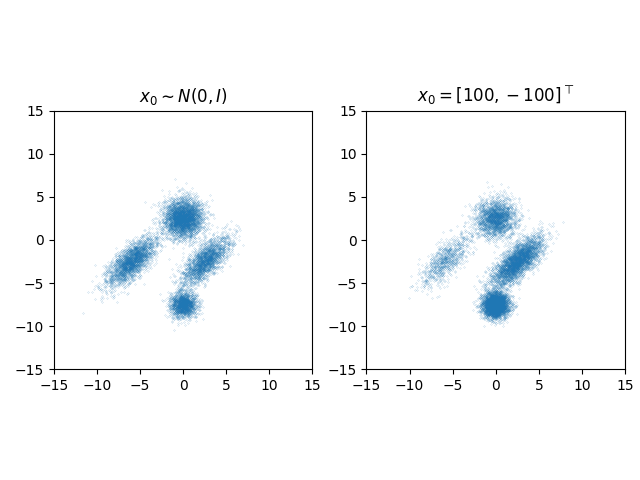
どちらの初期値でもメトロポリス・ヘイスティング法による左側の図と似たサンプリング結果になっており、2つ目の問題点である初期値が尤度の低い場所からサンプリングした場合の解決ができています。

推定されたスコアからのサンプリング

デノイジングスコアマッチングによるサンプリング

スコアを用いると初期値を気にせずともサンプリングを行うことができました。しかし、真の分布がわからないことが多いように、真のスコアもまたわからないことが多いです。ここからは学習データからスコアを推定し、それを用いてサンプリングする方法について見ていきます。

まず最初に思いつくのは、学習データのスコアとモデルの出力の2乗誤差を最小化することでモデルを学習できそうです。

$\displaystyle J_{\mathrm{ESM}}(\theta) = \frac{1}{2} \mathbb{E}_{p(x)} [|| \nabla_x \log p(x) - s_{\theta} (x) ||^2] .$

ここで $s_{\theta} (x)$ はパラメータ $\theta$ で特徴付けられたスコアを推定するモデルです。しかし、上述したとおりこの問題設定では真のスコアもわかりません。そこでいくつかの仮定をおいてこの式を変形していくと、目的関数は真のスコアを用いない以下の式で表すことができます。

$\displaystyle J_{\mathrm{DSM}}(\theta) = \frac{1}{2} \mathbb{E}_{\epsilon \sim \mathcal{N}(\boldsymbol{0}, \sigma^2 \mathrm{I}), x \sim p(x)} [||- \frac{\epsilon}{\sigma^2} - s_{\theta} (x + \epsilon, \sigma)||^2] .$

この目的関数を見ると、ノイズが加えられた入力から、分散でスケールされたノイズを予測する関数を学習しています。ここで行っていることはノイズが加えられた条件付き確率のスコア $\nabla_{x + \epsilon} \log p(x + \epsilon | x)$ と、 $s_{\theta} (x + \epsilon, \sigma)$ (ノイズを加えた $x$ を入力としてる)を一致するように学習させることですが、これは元々のデータ分布のスコアを学習することと一致します。

これで学習データさえあれば $s_{\theta}$ を学習できそうです。実際に学習させてサンプリングしてみましょう。今回は学習データとして上の図で見せた真の分布から正しくサンプリングしたデータを用いて学習しました。ランジュバン・モンテカルロ法の真のスコアをこの $s_{\theta}$ に置き換えてサンプリングした結果が以下の図になります。

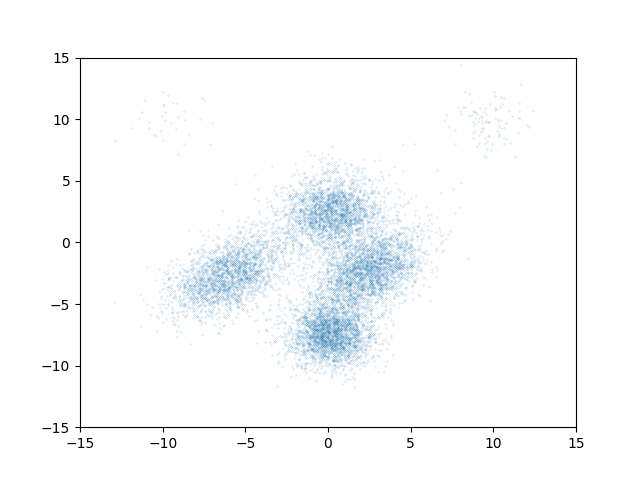
このように初期値を適切に設定した場合は、真のスコアを用いたランジュバン・モンテカルロ法によるサンプリングされた結果と似たサンプリング結果になっています。しかし、実は初期値が尤度の低い領域にある場合はうまくサンプリングできないことが多いです。スコアを用いると初期値を気にせずともサンプリングを行うことができるはずでしたが、どうしてでしょうか。それは学習データに尤度の低いデータがほとんど含まれていないので、尤度の低い領域でのスコアを学習することができないためです。

スコアベースモデルによるサンプリング

デノイジングスコアマッチングによるサンプリングでも2つの問題点を解決できていませんでした。スコアベースモデルはデノイジングスコアマッチングを改良することでその2つの問題点を解決しています。

デノイジングスコアマッチングの目的関数では、ノイズが加えられた条件付き確率のスコア $\nabla_{x + \epsilon} \log p(x + \epsilon | x)$ を予測してました。この $\epsilon$ を大きな分散 $\sigma^2$ をパラメータに持つ分布から生成することで、ノイズが加えられた条件付き確率は元のデータ分布よりもなだらかになります。そうすることで十分大きな $\sigma$ を用いると元々は確率がほとんど0になるような領域からでもスコアを学習でき、２つ目の問題点を解決できそうです。また、十分なだらかになることで、元々は多峰性のデータ分布だったとしても谷を乗り越えて他の山へ移ることができ、1つ目の問題点を解決できそうです。

そこでスコアベースモデルでは複数の大きさの分散を用意し、その分散ごとにノイズが加えられた条件付き確率のスコアを予測します。そうすることで十分になだらかな分布から段階的にサンプリングでき、2つの問題点を解決したサンプリングができます。スコアベースモデルの目的関数は $T$ 個のノイズの強さ $\sigma_1 \lt \sigma_2 \lt ... \lt \sigma_T$ と重み $w_t$ を用いて

$\displaystyle J_{\mathrm{SBM}}(\theta) = \sum^T_{t=1} w_t \mathbb{E}_{\epsilon_t \sim \mathcal{N}(\boldsymbol{0}, \sigma^2_t \mathrm{I}), x \sim p(x)} [||- \frac{\epsilon_t}{\sigma^2_t} - s_{\theta} (x + \epsilon_t, \sigma_t)||^2] ,$

と表せます。

サンプリングのコード例です。

class ScoreBasedModel(torch.nn.Module):
    ...
    def sample(self, sigmas, N, K=5000, alpha=0.1, device="cpu"):
        assert sigmas.dim() == 1
        with torch.no_grad():
            sorted_sigmas = sigmas.sort()[0].to(device)
            x = torch.randn(N, self.input_dim, device=device) * sorted_sigmas[-1]
            for t in sorted(range(len(sorted_sigmas)), reverse=True):
                alpha_t = alpha * sorted_sigmas[t] * sorted_sigmas[t] / (sorted_sigmas[-1] * sorted_sigmas[-1])
                noise_coeef = torch.sqrt(2 * alpha_t)
                for k in range(K):
                    if t == 0 and k == K - 1:
                        noise = torch.zeros(N, self.input_dim, device=device)
                    else:
                        noise = torch.randn(N, self.input_dim, device=device)
                    tmp_sigma = sorted_sigmas[t].unsqueeze(0).unsqueeze(1).expand(N, 1)
                    tmp_sigma_index = torch.tensor([t for _ in range(N)], device=device)
                    score =self.forward(x, tmp_sigma, tmp_sigma_index)
                    x = x + alpha_t * score + noise_coeef * noise
        return x

実際にサンプリングした結果がこちらです。

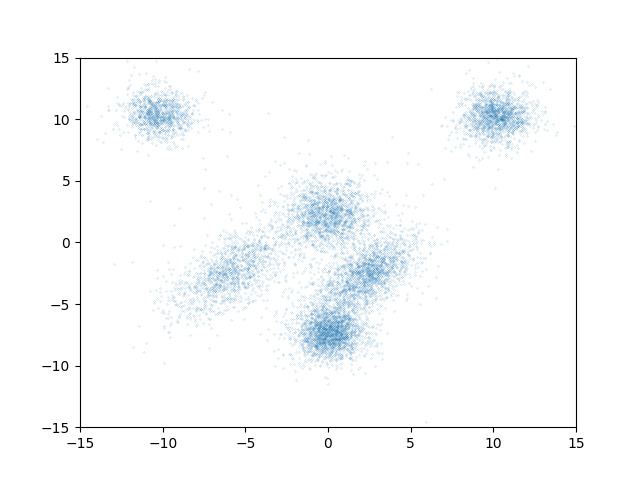
１つ目と2つ目の問題点を解決し、真の分布から正しくサンプリングされた結果と似ています。ちなみにコード例からもわかるとおりに、初期値は $\mathcal{N}(\boldsymbol{0}, {\sigma_T}^2\mathrm{I})$ 　から生成されており、今回は $\sigma _T = 100$ としてるので学習データが集まってる領域から遠く離れた領域に初期値があったとしても効率良く確率の高い領域へ到達できています。

デノイジング拡散確率モデルからのサンプリング

拡散モデルに関する解説記事は他にたくさんあるのでここではいきなり目的関数を示します。

$\displaystyle J_{\mathrm{DDPM}}(\theta) = \sum^T_{t=1} w_t \mathbb{E}_{\epsilon \sim \mathcal{N}(\boldsymbol{0}, \mathrm{I}), x \sim p(x)} [||\epsilon - \epsilon_{\theta} (\sqrt{\bar{\alpha}_t} x + \sqrt{1 - \bar{\alpha}_t} \epsilon, t)||^2] .$

この目的関数はスコアベースモデルの目的関数と重みが異なるだけで本質的に同じです。つまりデノイジング拡散確率モデルによるサンプリングでも１つ目と2つ目の問題点を解決できています。

実際にモデルを学習し、サンプリングした結果がこちらです。

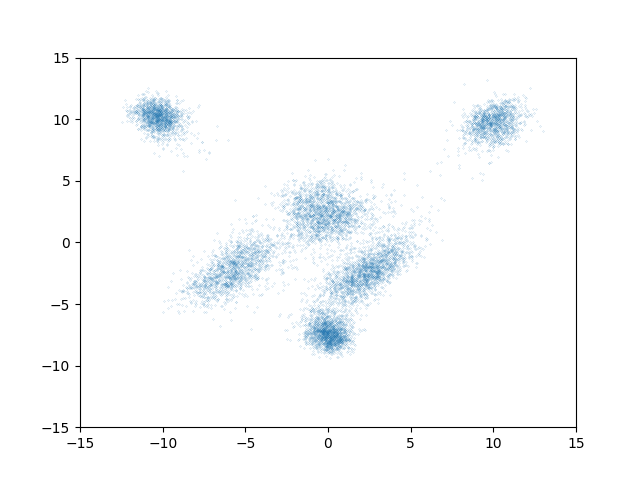
スコアベースモデルと同じく綺麗にサンプリングできています*1。

まとめ

この記事ではサンプリング手法としてよく使われるメトロポリス・ヘイスティングス法の問題点を２つあげて、その内の1つがスコアを用いたランジュバン・モンテカルロ法により解決されること、さらに複数のノイズの強さを用いてスコアを学習することによりどちらの問題点も解決できていることを簡単な例で確認しました。

この記事で使用したコードはこちらにあります。 https://github.com/tomoris/diffusion_models

*1:ちなみに学習データがサンプリング時の初期値から遠い場合も試してみました。デノイジング拡散確率モデルのサンプリングの初期値は $\mathcal{N}(\boldsymbol{0}, \mathrm{I})$ に従ってるため、学習データを $[-100, 100]^\top$ 並行移動したデータを用いて学習を行いましたが、うまくサンプリング出来ませんでした。デノイジング拡散確率モデルの論文を確認すると、学習データを先に [-1, 1] の区間にスケーリングしていたので、適切な前処理が必要みたいです。

VISASQ Dev Blog

ビザスク開発ブログ

拡散モデルのサンプリング性能の良さを体感してみる